§ Description

Link.

• 游戏在 $4\times4$ 的菱形棋盘上进行；

• 两名玩家轮流放置弹珠，可以在横向、纵向、$45$ 度斜线、$135$ 度斜线方向未放置弹珠的位置连续放置 $1$ 至 $3$ 颗弹珠，玩家在可以放置弹珠的情况下，必须至少放置 $1$ 颗弹珠。

• 如果某位玩家无法再继续放置弹珠，则该名玩家输掉游戏，另外一名玩家获胜。

§ Solution

虽然是套路，但毕竟是之前没做过的套路，写篇题解记一下。

首先我们可以直接考虑状压，棋盘编号见图：

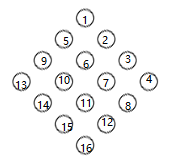
然后你打个表出来，表示所有能走的情况（状压），比如我要放棋子在 $1-5-9$ 上面，就是 $(100010001)_{2}$。

因为是用 C++ 输出的形式手打的 $82$ 种情况表，所以 generator 就不附了。

然后你打个 DP，设 $f_{S}$ 为当前棋盘状态为 $S$（$S$ 的第 $i$ 为 $1$ 表示这个格子被占据，反之亦然）是先手必胜还是先手必输或者不知道（分别对应数字 $1/0/-1$）。

初始状态为 $\forall i\in[0,2^{n}-1),f_{i}=-1$；$f_{2^{n}-1}=0$。

然后你记搜一下，把所有状态搜出来。

然后就回答询问即可，只是不太清楚为什么要搞这么多字符读入卡 IO，明明多不多组都一样。

#include<bits/stdc++.h>
using namespace std;
int t,n=7,m[8]={1,2,3,4,3,2,1},id,f[(1<<16)+10];
char s[10];
const int upper=(1<<16);
const int ID[10][10]={{0},{4,1},{8,5,2},{12,9,6,3},{13,10,7},{14,11},{15}};
const int walking[90]={1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768,17,3,18,272,48,34,6,288,36,4352,768,544,96,68,12,4608,576,72,12288,8704,1536,1088,192,9216,1152,24576,17408,3072,2176,18432,49152,34816,33,528,66,8448,1056,132,16896,2112,33792,136,273,7,1057,4368,16912,112,546,2114,14,292,1792,8736,224,33824,1092,4672,584,28672,3584,17472,2184,9344,57344,34944};
inline int unionset(int x,int y){return x|y;}
inline int intersection(int x,int y){return x&y;}
inline bool emptyset(int x){return x==0;}
void dfs(int board)
{
	if(~f[board])	return;
	for(int i=0;i<82;++i)
	{
		if(emptyset(intersection(board,walking[i])))
		{
			int newset=unionset(board,walking[i]);
			dfs(newset);
			if(f[newset]==0)
			{
				f[board]=1;
				return;
			}
		}
	}
	f[board]=0;
}
inline char fgc()
{
	static char buf[1<<17],*p=buf,*q=buf;
	return p==q&&(q=buf+fread(p=buf,1,1<<17,stdin),p==q)?EOF:*p++;
}
inline char fgop()
{
	char res=0;
	while((res^'*')&&(res^'.'))	res=fgc();
	return res;
}
inline void read(int &x)
{
	x=0;
	char c=fgc();
	while(isdigit(c)==0)	c=fgc();
	while(isdigit(c))	x=(x<<3)+(x<<1)+(c^'0'),c=fgc();
}
int main()
{
	read(t);
	memset(f,-1,sizeof(f));
	f[upper-1]=0;
	for(int i=0;i^upper;++i)
	{
		if(f[i]==-1)	dfs(i);
	}
	while(t--)
	{
		int board=0;
		for(int i=0;i<n;++i)
		{
			for(int j=0;j<m[i];++j)	board+=(fgop()=='*')?(1<<ID[i][j]):0;
		}
		printf(f[board]?"Possible.":"Impossible.");
		printf("\n");
	}
	return 0;
}