☆ 0x01 引子

首先引入这样一种问题：给定 $n$ 的范围，再给出一个长度为 $n$ 的序列，然后给出各种询问，询问的数量大于 $n$ 。比如说 $n=10^{6},q=10^{7}$ 。

考虑线段树， $\log n$ 的查询当场死亡。

那么怎么办呢？猫锟大大就给出了一种 不支持修改但是可以做到 $\Theta(n\log n)$ 预处理 $\Theta(1)$ 查询的数据结构——猫树 ，给大家分享一下原文章Link。

☆ 0x02 预处理部分

∆ 具体过程

按我的理解，猫树其实可以看做像 $DP$ 一样 把分治的过程记录下来 的东西。

举例来说，我们现在需要你查询序列的区间最大值和区间和之类的 具有区间可加性 的信息，查询区间为 $[l,r]$ 。

递归的来想，区间 $[l,r]$ 是由区间 $[l,mid]$ 和 $[mid+1,r]$ 两个区间合并而来的，那么我们是否能够**使用预处理的手段使得所有可能的询问区间都可以通过合并来 $\Theta(1)$ 得出答案呢？**答案是没问题。

接下来我们看看具体的步骤：

step1:我们将整个序列分为两部分，即 $[1,mid]$ 和 $[mid+1,n]$

step2:分别从 $mid$ 向左从 $mid+1$ 向右，遍历整个区间

step3:维护信息。比如说区间最大值，那么对于从 $mid$ 开始向左的区间， $maxvalue_{i}=max\{max_{i+1},a_{i}\}$ ，对于从 $mid+1$ 开始向右的区间同理

step4:复读机

∆ 时间复杂度

就像线段树一样，猫树是一颗二叉树，深度最多为 $\log_{2}n$ 层，每一层我们需要 $\Theta(n)$ 的时间进行维护信息的工作，所以预处理的时间复杂度为 $\Theta(n\log n)$ 。

啊对了，空间复杂度也是 $\Theta(n\log n)$ ，想想就明白了，这里为了节省篇幅就略掉了。

☆ 0x03 处理询问部分

∆ 具体过程

对于一个询问区间，我们可以把它放在某个 已经经过预处理的 并且询问区间经过 已经经过预处理的 的区间的中点的区间里。简而言之，我们设询问区间为 $q$ ，我们把 $q$ 放在一个区间 $t$ 里面， $t$ 的定义是已经经过预处理，并且询问区间 $q$ 跨过区间 $t$ 的中点。

为什么呢？其实很简单，既然 $t$ 已经经过了预处理，那么 $t$ 的中点把 $q$ 分成的两部分也一定经过了预处理，我们就可以 $\Theta(1)$ 的合并了。

没有图始终没有感觉对吧？那么上图来理解吧。

这是一棵牛逼的树，我们给他取名叫牛逼树

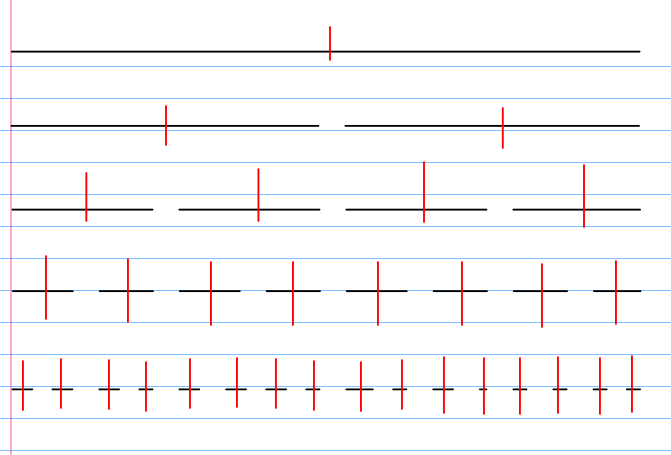
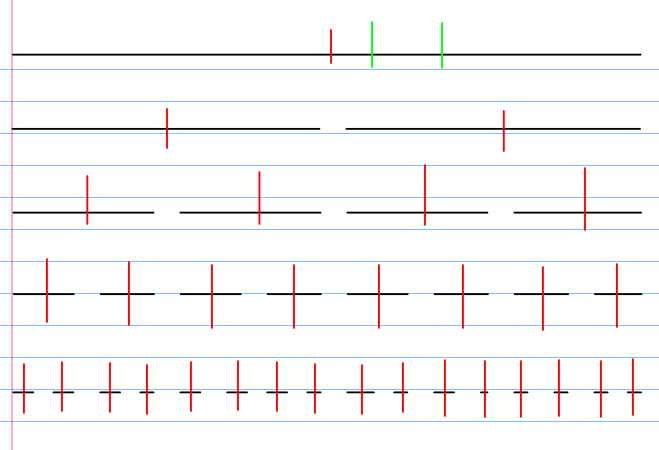
img spfaed

哦！现在牛逼树上有了一个询问！

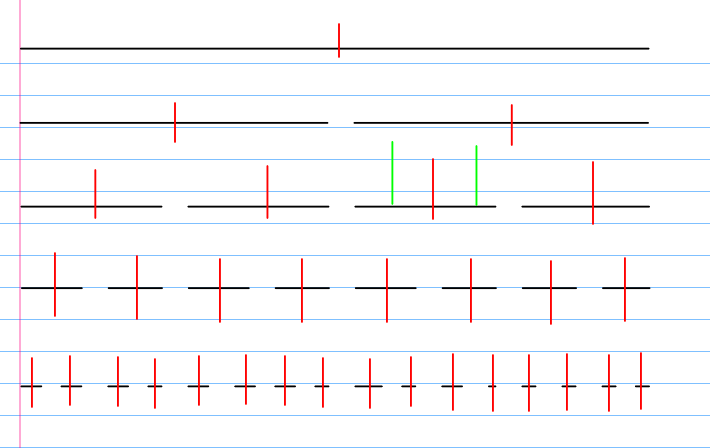
img spfaed

哈！牛逼树上的询问成功的被第三层的某个区间分割啦！耶！

img spfaed

~~平生没有这么傻过~~

∆ 时间复杂度

查询的复杂度貌似是 $\Theta(\log n)$ ？不不不，既然前面说了查询是 $\Theta(1)$ 的，那就一定是。接下来我们谈一谈优化的内容。

∆ 时间复杂度优化

仔细想想如果我们不从根结点出发，而是从叶子结点来的话，这就是在求两个结点的 $LCA$ 嘛！但是有什么用呢？仔细想想，我们的牛逼猫树是一颗二叉树，而二叉树的 $LCA$ 是什么？

这里有一个重要的性质，二叉树两个结点的 $LCA$ 就是二进制下的它们的编号的 最长公共前缀 。

比如说 $7$ 号结点和 $5$ 号结点的 $LCA$ 就是：

$(0111)_{2}\ \ \ (0101)_{2}$ 也就是 $(01)_{2}$ 也就是 $1$ 号结点。

那么我们如何找出两个数的二进制最长公共前缀呢？

我们可以发现，我们将两个节点 $xor$ 起来，就能够去掉它们的最长公共前缀。于是我们就可以使用x>>log2[x^y]来获得两个结点的 $LCA$ 。

☆ 0x03 例题与代码

∆ # SP1043 GSS1 - Can you answer these queries I

给出了序列 $A[1],A[2],…,A[N]$ 。 ( $a[i]≤15007,1≤N≤50000$ )。查询定义如下：查询 $(x,y)=\max\{a[i]+a[i+1]+...+a[j];x≤i≤j≤y\}$ 。给定 $M$ 个查询，程序必须输出这些查询的结果。

题目让我们查询最大子段和，并且没有修改操作，我们可以通过猫树来玩这道题。

具体步骤上文已经写了，对于这道板题，我们可以直接记录最大子段和以及最大前缀和即可。

代码：

// 省略了一些头文件、快读、预处理命令等东西，完整代码请移步至https://vjudge.net/solution/24123955

const int SIZE = 2e5 + 5;
const int LOG_SIZE = 20;

int n, m, real = 2, ints[SIZE];
// real:把n映射为2的幂形式
// ints:原序列
namespace CatsTree {
	int log2[SIZE]; // 预处理log2
	int nodes[SIZE]; // 结点
	int ans[LOG_SIZE][SIZE]; // 最大子段和
	int preans[LOG_SIZE][SIZE]; // 最大前缀和
	
	void MakeLog() {
		for (int i = 2, lim = real << 1; i <= lim; ++i) log2[i] = log2[i >> 1] + 1;
	}
	
	void BuildTree(int k, int l, int r, int s) {
		if (l ^ r) {
			ans[s][mid] = preans[s][mid] = ints[mid];
			int pre, sum;
			pre = sum = ints[mid];
			sum = sum > 0 ? sum : 0;
			for (int i = mid - 1; i >= l; --i) {
				pre += ints[i];
				sum += ints[i];
				ans[s][i] = max(pre, ans[s][i + 1]);
				preans[s][i] = max(sum, preans[s][i + 1]);
				sum = sum > 0 ? sum : 0;
			}
			ans[s][mid + 1] = preans[s][mid + 1] = ints[mid + 1];
			pre = sum = ints[mid + 1];
			sum = sum > 0 ? sum : 0;
			for (int i = mid + 2; i <= r; ++i) {
				pre += ints[i];
				sum += ints[i];
				ans[s][i] = max(pre, ans[s][i - 1]);
				preans[s][i] = max(sum, preans[s][i - 1]);
				sum = sum > 0 ? sum : 0;
			}
			BuildTree(ls, l, mid, s + 1);
			BuildTree(rs, mid + 1, r, s + 1);
		}
		else nodes[l] = k;
	}
	
	int GetAnswers(int l, int r) {
		if (l ^ r) {
			int s = log2[nodes[l]] - log2[nodes[l] ^ nodes[r]];
			return max(ans[s][l] + ans[s][r], max(preans[s][l], preans[s][r]));
		}
		else return ints[l];
	}
}
#define CT CatsTree

void init() {
	read(n);
	while (real < n) real <<= 1;
	for (int i = 1; i <= n; ++i) read(ints[i]);
	CT::BuildTree(1, 1, real, 1);
	CT::MakeLog();
}

void solving() {
	read(m);
	for (int i = 0, l, r; i < m; ++i) read(l, r), write(io_l, CT::GetAnswers(l, r));
}

signed main() {
	init();
	solving();
}