☆ 0x00

// 我把这题当做莫队模板应该没问题吧...

☆ 0x01

考虑这样一个问题：

对于一个序列 $A_1,A_2,\cdots,A_n$ ，有如下询问

形如 $S\ \ l\ \ r$ 的命令表示对区间 $[l,r]$ 求和，并输出

形如 $Q\ \ l\ \ r$ 表示 $\cdots$

本题不强制在线

对于这样的静态问题，我们可以考虑用莫队来解决。据说莫队支持修改~~但我太弱不会~~

现在你有区间 $[3,5]$ 的和，可以求 $[3,6]$ 的区间和吗？显然，将 $[3,5]$ 的区间和加上 $A_6$ 即可。类似的，求 $[2,4]$ 的区间和，我们只需减去 $A_5$ 即可。

可以结合下图感知一下

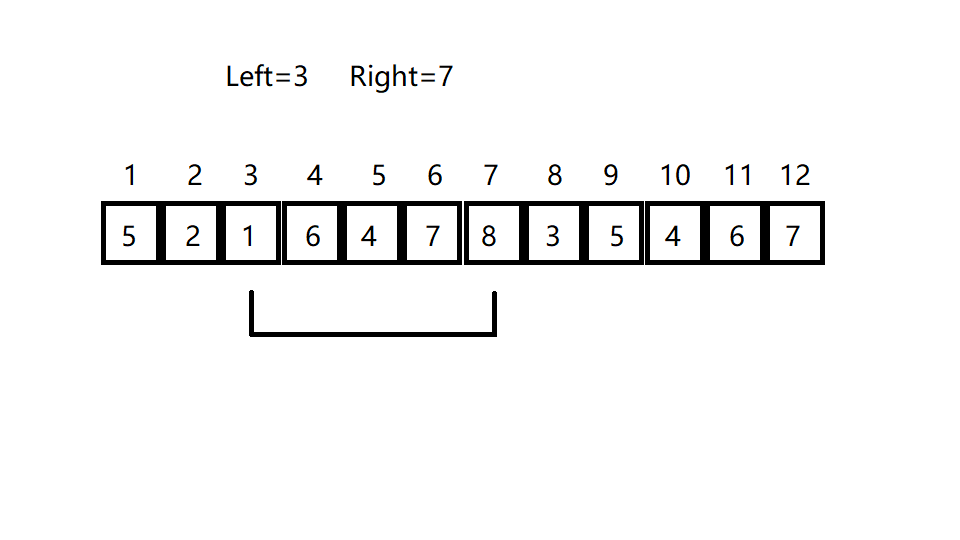
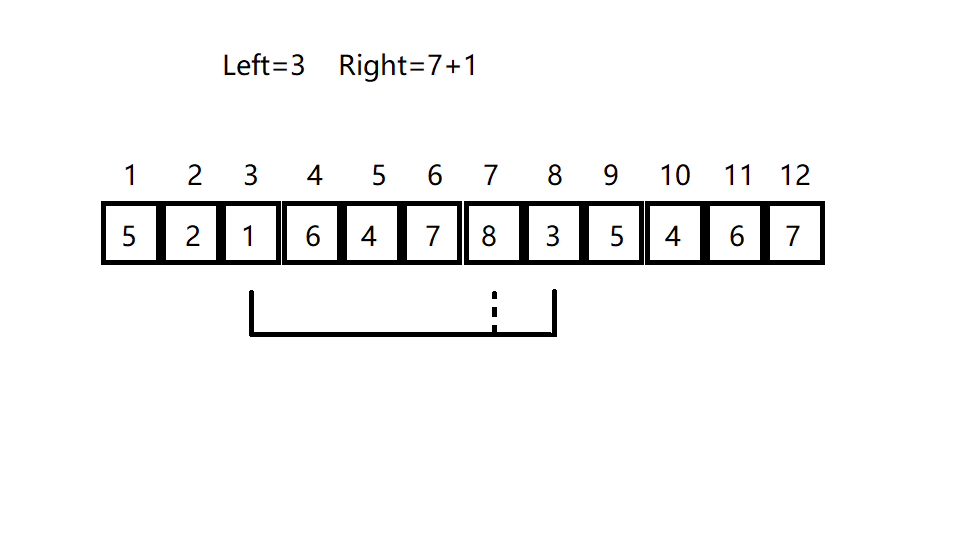
☆ 0x02

好，接下来我们想一下如何维护这种询问之间的关系。

很容易想到排序，首先我们对询问的左端点进行排序。再把整个询问序列分为 $\sqrt{n}$ 块，每块以内再按右端点排序。

所以我们可以得出以下结论：

莫队就是对于一系列的询问，通过排序减小询问的之间的差距，然后以计算贡献的方法离线的得出答案

☆ 0x03

来一道简单的例题

∆ 小B的询问

小B 有一个长为 $n$ 的整数序列 $a$ ，值域为 $[1,k]$ 。
他一共有 $m$ 个询问，每个询问给定一个区间 $[l,r]$ ，求：

其中 $c_i$ 表示数字 $i$ 在 $[l,r]$ 中的出现次数。
小B请你帮助他回答询问

这道题让我们求

$\sum\limits_{i=1}^k c_i^2$

开一个桶，计算每个数出现的次数，所以我们可以由此计算答案的贡献，就可以写出以下的代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#include <cmath>

using namespace std;

const int SIZE = 5e4 + 5;
struct QueryNode {
	int l, r;
	int id; // 储存询问的顺序，方便输出
} Q[SIZE];
int a[SIZE], n, m, k, pos[SIZE];
int cnt[SIZE], ans[SIZE], res;

// a:原序列
// pos:每个位置所处的块
// cnt:桶
// ans:询问的答案
// res:每次调整所得到的贡献

inline void add(int x) { cnt[a[x]]++, res += cnt[a[x]] * cnt[a[x]] - (cnt[a[x]] - 1) * (cnt[a[x]] - 1); }

inline void del(int x) { cnt[a[x]]--, res -= (cnt[a[x]] + 1) * (cnt[a[x]] + 1) - cnt[a[x]] * cnt[a[x]]; }

signed main() {
	scanf("%d %d %d", &n, &m, &k);
	int block = sqrt(n);
	for (int i = 1; i <= n; ++i) scanf("%d", &a[i]), pos[i] = i / block;
	for (int i = 1; i <= m; ++i) scanf("%d %d", &Q[i].l, &Q[i].r), Q[i].id = i;
	sort(Q + 1, Q + 1 + m, [](QueryNode x, QueryNode y) { return pos[x.l] ^ pos[y.l] ? pos[x.l] < pos[y.l] : x.r < y.r; });
	int l = 1, r = 0;
	for (int i = 1; i <= m; ++i) {
		while (l > Q[i].l) add(--l); // 这四句都是在对当前的区间对于询问的区间进行调整
		while (r < Q[i].r) add(++r); // 这三句都是在对当前的区间对于询问的区间进行调整
		while (l < Q[i].l) del(l++); // 这二句都是在对当前的区间对于询问的区间进行调整
		while (r > Q[i].r) del(r--); // 这一句都是在对当前的区间对于询问的区间进行调整
		ans[Q[i].id] = res;
	}
	for (int i = 1; i <= m; ++i) printf("%d\n", ans[i]);
	return 0;
}

☆ 0x04

其实莫队是有套路的，基本上莫队的题都是这样的:

	for (int i = 1; i <= m; ++i) {
		while (l > Q[i].l) add(--l);
		while (r < Q[i].r) add(++r);
		while (l < Q[i].l) del(l++);
		while (r > Q[i].r) del(r--);
		ans[Q[i].id] = res;
	}

我们只需考虑 $add$ 函数以及 $del$ 函数即可