哲学题。

以下标为横轴，$p_i$ 为纵轴，画出一个坐标系。然后你会发现每个点的后继在其右上方，以此为依据来分层（具体来说，就是求出每个位置的 LIS）。

我毛了张图给你看啊：

。

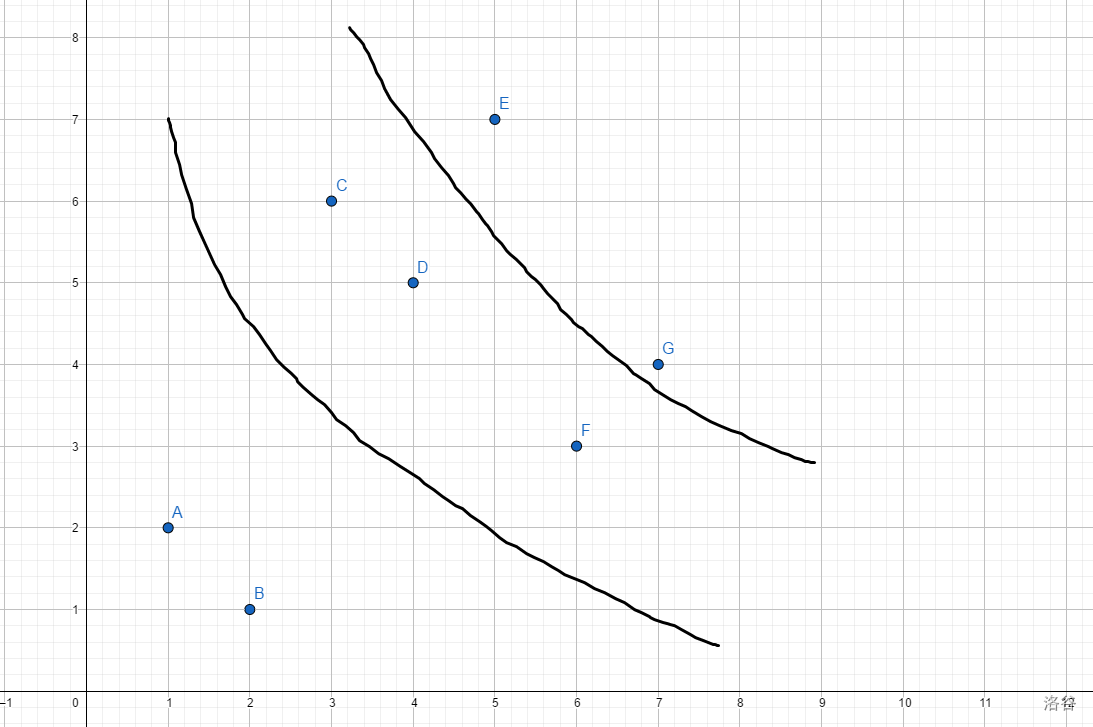然后在每层搞事情。这里有个结论：

Claim：存在一种选择 LISs 的方案，使得每个 LIS 都不交叉。

证明应该不难吧，因为每两个之间交换了没有影响，每层都看得到。那么选择下标更小的点一定苏卡不劣。然后优化下搜索的方式就可以解决了，这个具体看代码。

int n,a[1000100],fwt[1000100],dp[1000100],st[1000100],ed[1000100],q[1000100],lis,ans,lst[1000100];
vector<int> rec;
void Add(int x,const int w) { for(; x<=n; x+=x&-x)	cmax(fwt[x],w); }
int Sum(int x) { int res=0; for(; x; x^=x&-x)	cmax(res,fwt[x]); return res; }
void digger() {
	printf("%d %d\n",ans,lis);
	for(int i=1; i<=ans; ++i) {
		for(int j=(i-1)*lis+1; j<=i*lis; ++j)	printf("%d ",rec[j-1]);
		puts("");
	}
	exit(0);
}
signed main() {
	n=read();
	for(int i=1; i<=n; ++i) {
		dp[i]=Sum((a[i]=read())-1)+1;
		Add(a[i],dp[i]),cmax(lis,dp[i]);
		ed[dp[i]]++;
	}
	for(int i=1; i<=n; ++i)	ed[i]+=ed[i-1],st[i]=ed[i];
	for(int i=n; i; --i)	q[st[dp[i]]--]=i;
	for(int i=1; i<=n; ++i)	st[i]=ed[i-1]+1;
	for(int i=1; i<=n; ++i)	sort(q+st[i],q+ed[i]+1);
	while(233) {
		for(int i=1; i<=lis; ++i) { // enumrating layers
			if(st[i]>ed[i])	digger();
			if(a[q[st[i]]]<a[lst[i-1]]) {
				----i; st[i+1]++;
				continue;
			}
			while(q[st[i]]<lst[i-1] && st[i]<=ed[i]) {
				st[i]++;
				if(a[q[st[i]]]<a[lst[i-1]]) {
					----i; st[i+1]++;
					goto Suc;
				}
			}
			if(st[i]>ed[i])	digger();
			lst[i]=q[st[i]];
			Suc:;
		}
		for(int i=1; i<=lis; ++i)	rec.push_back(lst[i]),st[i]++;
		ans++;
	}
	return 0;
}